Utilisation des parenthèses

EXEMPLE DE SITUATION :

Cinq élèves de la classe de 7^ème année de l’EB de l’institut de Mpese au Kongo-central, décident de créer une caisse afin de résoudre le problème de casse-croûte pendant la récréation. Au bout d’une semaine, la situation de mise et de retrait de chacun se présente de la manière suivante :

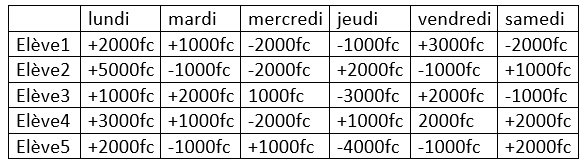
Le lundi suivant, l'enseignant demande à tous les élèves de la classe de calculer la part qui revient à chacun de ces cinq élèves en utilisant les paraenthèses.

1. Vérification des connaissances précédentes

a) calculer 

1. (+25)+(+13)+(-20)
2. (-1)-(-3)-(+2)
3. -28-2+15

b) énoncer la règle de signe de la somme de deux entiers relatifs.

2. Motivation( Découverte)

Demander aux élèves de:

• Lire la situation en silence, ensuite à haute voix par deux élèves choisis.
• Expliquer la situation en ses propres termes.

Organisation de la classe et consigne:

• Amener les élèves à se grouper à deux ou trois.
• Consigne:  a) lire le tableau de la situation

b) identifier:

• les objets
• les actions à mener pour calculer la par qui revient à chacun des cinq élèves

Question de récapitulation:

- Restituer la règle de l'introduction ou de la suppression des parenthèses (crochets ou accolades précédées d'un signe.

(1): Vérification des acquis sur les savoirs essentiels:

a) rappeler la définition de la soustraction dans Z.

b) dégager la règle de suppression et d'introduction d'une parenthèse précédée du signe -.

c) Calculer les expressions suivantes:

1.  [(+5)+(-8)]-[(-2)-(-1)]
2. [(-12)+(-4)]-(-7)+(-9)

(2): Proposition d'une situation similaire

Traiter la situation ci-dessus si les opérations de cinq élèves s'arrêtent le jeudi.

a) 

1. 18
2. 0
3. -15

b)

- la somme de deux entiers de même signe est un entier de même signe que les deux premiers.

- la somme de deux entiers de signes contraires est un entier dont le signe est celui de l'entier ayant la grande partie numérique.

2. Compréhension de la situation

• lecture de la situation en silence, ensuite à haute voix.
• Explication de la situation par deux élèves.

Activités sur le tableau de spécification:

a) lecture du tableau de la situation.

b) identification 

• des objets (nombres relatifs).
• actions à mener:
  • Application des règles de signes pour l'addition et la soustraction.
  • Introduction et suppression des parenthèses dans une expression donnée.
  • Traitement d'une expression contenant des parenthèses.
  • calcul de la part de chacun de 5 élèves

Participation des élèves à la production de la synthèse:

• On peut introduire ou supprimer des parenthèses (crochets ou accolades) précédées du signe:
  • (+): sans changer les signes des termes à l'intérieur de ceux-ci.
  • (-): à condition de changer les signes de tous les termes à l'intérieur de ceux-ci.

Réponses aux questions (items)

a) la différence de deux entiers relatifs est la somme du premier entier avec l'opposé du second : a-b=a+(-b)

b) on peut introduire ou supprimer des parenthèses, crochets et accolades précédés du signe:

• (+) sans changer les signes des termes à l'intérieur de ceux-ci.
• (-) à condition de changer les signes de tous les termes à l'intérieur de ceux-ci.

1. -2
2. -18