

Rappel
Calculez : log5−4log3+3log3+log2log4−log2
Rappel
log5−log34+log33+log2log42=log5+log27+log2−log34log4/2log5.27.2812=270812=log1032=log103.12=log106
Motivation
Quel est l’exposant de ce logarithme ?
log2(x+1)?
Motivation
L’exposant de ce logarithme est x+1.
Que représente x+1 en algèbre ?
X+1 représente l’équation.
Annonce du sujet
Qu’allons-nous étudier aujourd’hui en math ?
Annonce du sujet
Aujourd’hui nous allons étudier les équations logarithmiques.
Qu’est-ce qu’une équation logarithmique ?
Equations logarithmiques
a. Définition : une équation logarithmique est toute équation où l’inconnue intervient dans l’expression du logarithme.
Comment peut-on résoudre une équation logarithmique ?
b. Résolution : Pour résoudre une équation logarithmique, on procède comme suit :
- poser les conditions d’existence des solutions de l’équation.
- Ramener éventuellement les logarithmes à la même base.
- utiliser les propriétés des logarithmes pour obtenir loga4 = logav <=> u = v.
- retenir les valeurs de l’inconnue qui vérifie les conditions posées ci-dessous
Exemple : Résoudre dans IR, l’équation logarithmique suivante : log(x+1) =log32
Cp : x+1 ˃ 0
<=> x > -1

] -1, +∞ [
log3(x+1)=log32 <=> x+1 =2
<=> x = 2-1
X = 1
S = {1}
Résoudre dans IR, les équations ci-dessous :
a.log2(x+14)+log2(x+2)=6
Condition : x+14 ˃ 0
x˃ -14
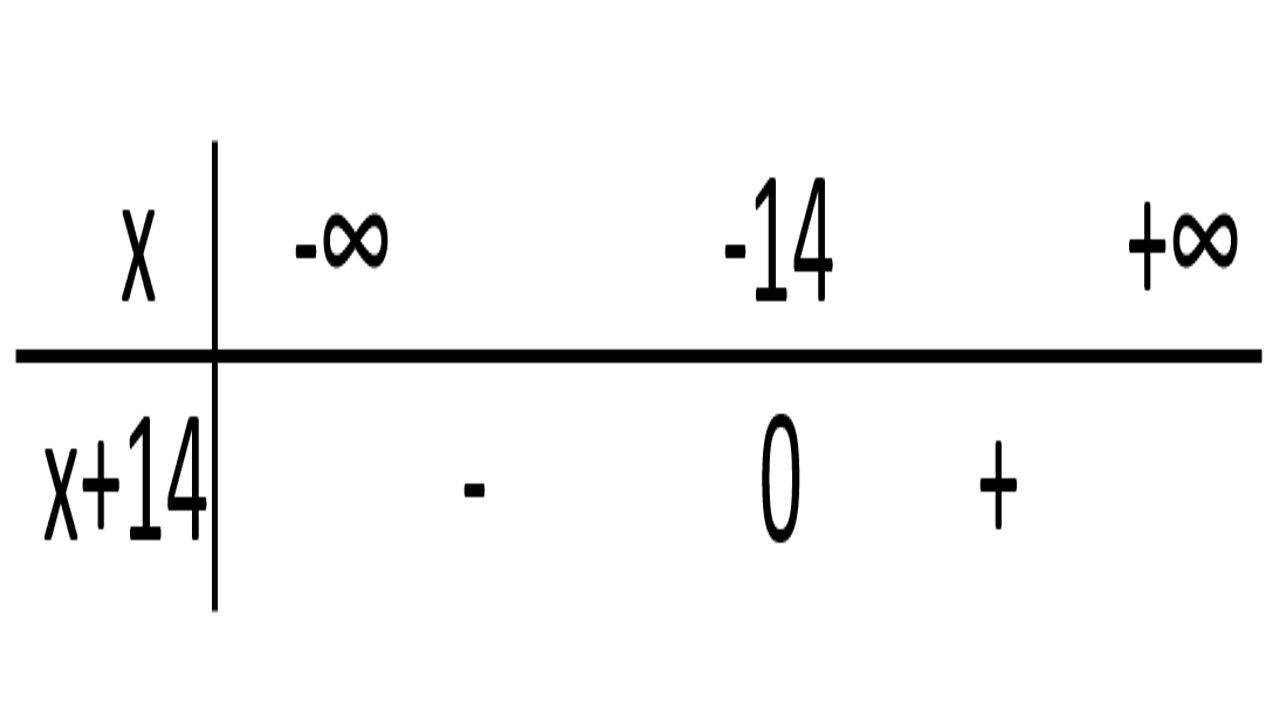
] -14, +∞ [
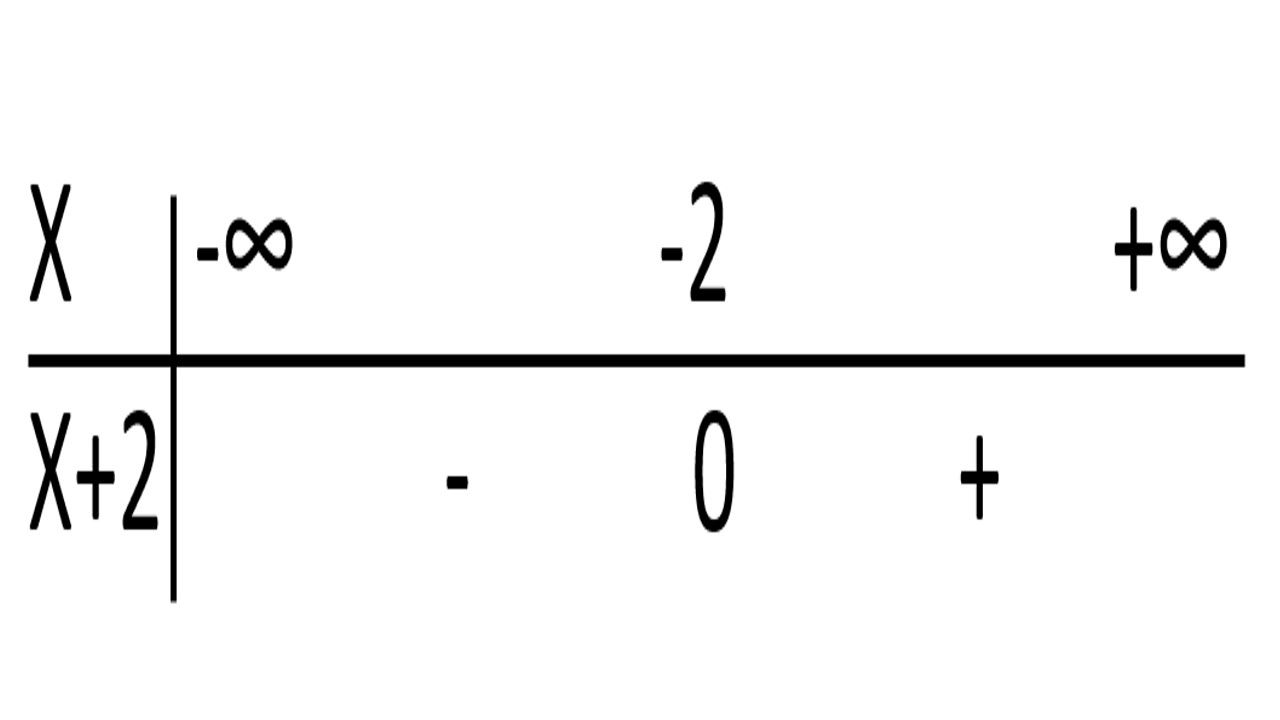
] -2, +∞ [
log2(x+14)(x+2)=6log22
X²+2x+14x+28 = 64
X²+16x+28-64 = 0
=16²-4(1)(-36)
= 256+144
= 400
\sqrt[]{∆} = ±\sqrt[]{400}
= ±20
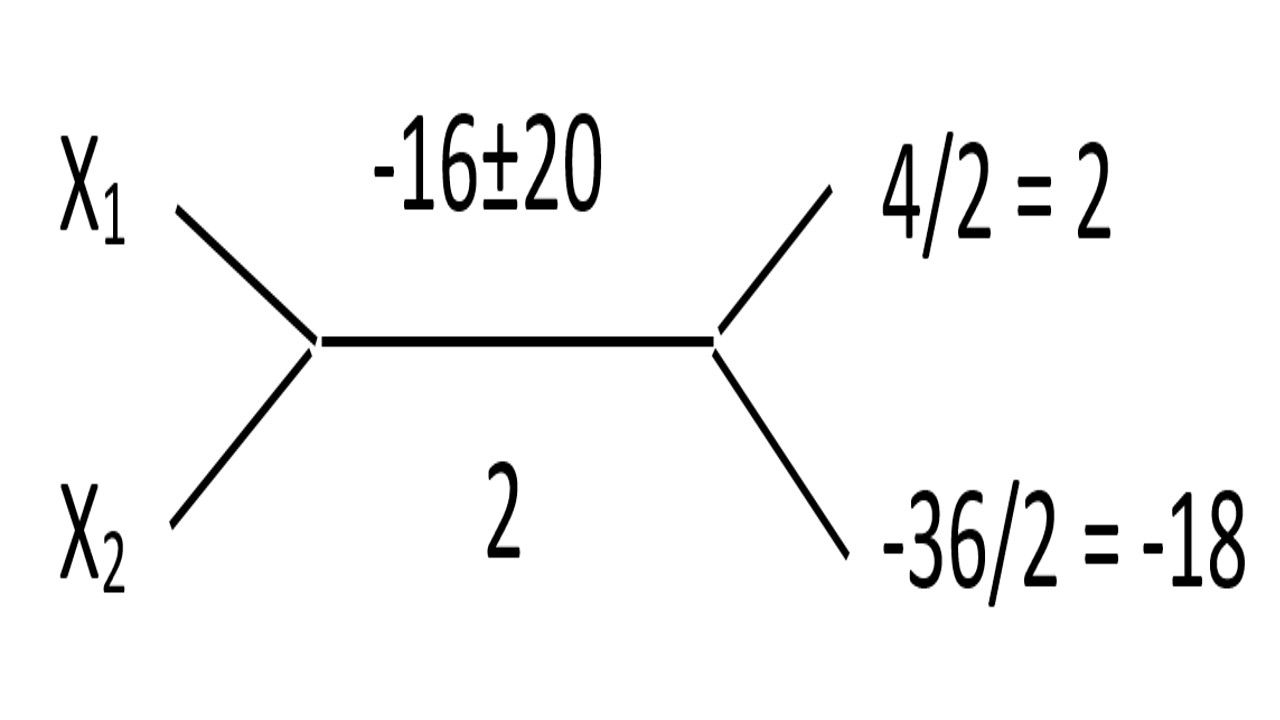
S = {2} seul le réel 2 vérifie la condition posée.
Résoudre dans IR, l’équation suivante :
log_3x= 1/2 + log_9 (4x+15)
X ˃ 0 et 4x+15 ˃ 0
X ˃ -15/4
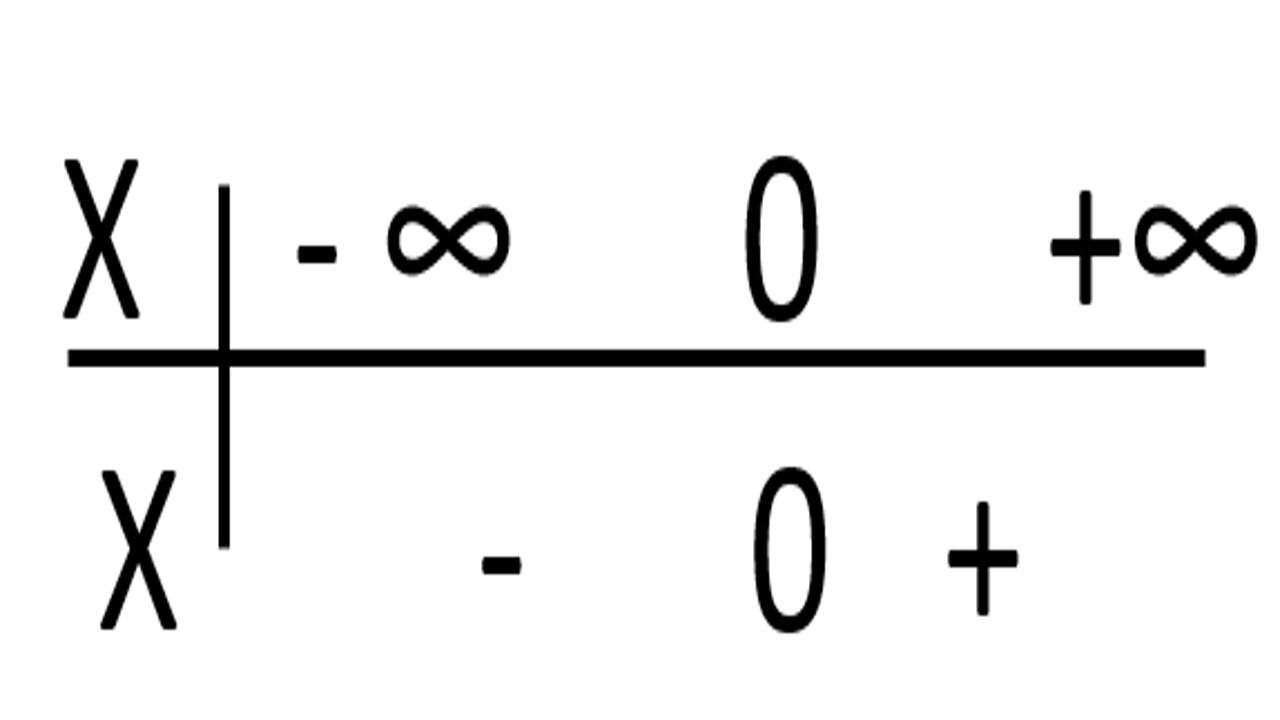
]0, +∞[
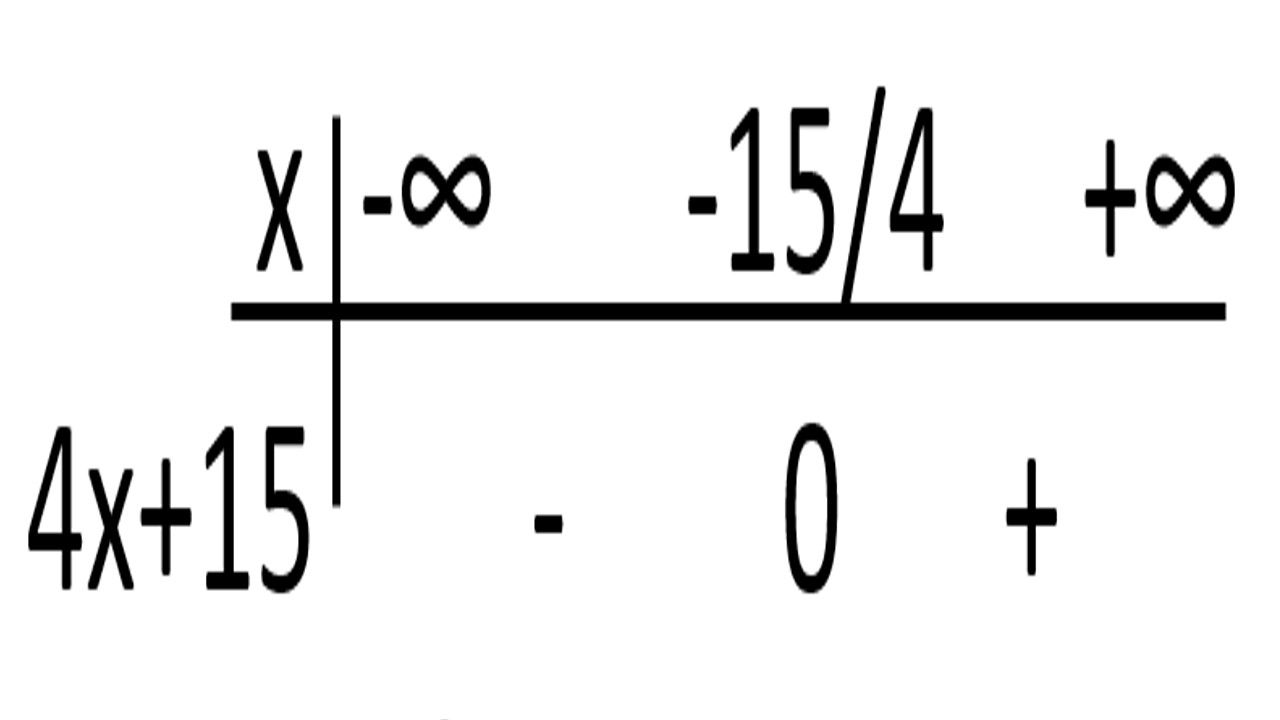
] -15/4, +∞[
log_3 x = ½ log_3 3+log_3 2 (4x+15)\\ log_3 x=1/2 log_3 3+1/2 log_3 4x+15\\ 2log_3 x = log_3 3 (4x+15)\\ log_3 x^2 = log_3 12x+45\\ X²-12x-45 = 0\\ ∆ = 144-4(1)(-45)\\ = 144+180\\ \sqrt[]{∆} = ± \sqrt[]{324}\\ = ±18

S = {15}