Exemple de situation :
Après la distribution des programmes Éducatifs du DAS dans une école, un élève trouve sur un emballage écrit : « Trois nombres complexes ont pour images les points sommets d’un triangle équilatéral dans le cercle de centre O et de rayon 2. Sachant que le premier de ces nombres a pour argument π/2 ». Il ramène cet emballage auprès de son enseignant de mathématiques. L’enseignant demande à ses élèves de calculer le troisième nombre complexe sous forme algébrique.
1. VERIFICATION DES CONNAISSANCES PRECEDENTES
1. écrire les nombres complexes sous formes cartésienne:
a) z1=i-7/3+7i
b) z2=1+18i/3+4i + 7-26i/3-4i
2. Démontrer que si λ est un réel, alors le nombre complexe
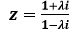a pour module 1.
3. Calculer:
a) le conjugué de l'opposé z= 1+2i/1+2i
b) le conjugué de l'inverse de z= 2i/3+2i
c) l'opposé du conjugué de z= (3-2i)2 - (2-3i)
d) l'inverse du conjugué de z= (1-4i) (1+4i) - (14+2i)
e) le conjugué du conjugué de l'opposé de
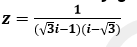
2. MOTIVATION (découverte)
l'enseignant demande aux élèves de (d'):
-lire la situation en silence, ensuite à haute voix par deux ou trois élèves;
-expliquer la situation en leurs propres termes.
ACTIVITES PRINCIPALES
Organisation de la classe et consigne
-Regroupement des élèves à cinq groupes
-consigne:
1. Représenter géométriquement les points images de ces trois nombres complexes de manière à obtenir un triangle équilatéral sachant que le premier nombre complexe a pour argument n/2;
2. Exprimer le troisième nombre complexe sous forme algébrique
III. SYNTHESE
Questions de récapitulation
Q1. Représenter un nombre complexe géométrique dans le plan Gauss.
Q2. Calculer l'argument d'un nombre complexe non nul.
Q3. Ecrire un nombre sous sa forme trigonométrique ou exponentielle.
Q4. Effectuer les opérations: le produit, le quotient, la puissance nième et la racine nième de nombre complexe non nul en utilisant la forme trigonométrie d'un nombre complexe.
REPONSES DES ELEVES AUX QUESTIONS:
a) z1=(i-7)(3-7i)/(3+7i)(3-7i), 3-7i étant le conjugué de 3+7i
D'où z1= -7/29 + 26/29i
b) Ici la réduction au même dénominateur est intéressant car 3+4i =3-4i
z2 = (1+18i)(3-4i) + (7-26i)(3+4i)/(3+4i)(3-4i)
= 3-4i+54i+72+21+28i-78i+104/9+16
= 200/25= 8 z2=8 avec a=8et b =0
2. Nous avons:
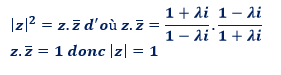
ATTENTION: pour tout
Nous avons:
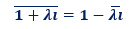
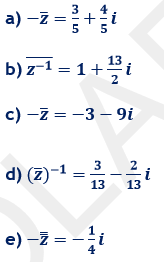
Compréhension de la situation
-lecture de la situation en silence et à haute voix par un ou deux élèves désignés;
-exploitations données par deux ou trois élèves et adoption par toute la classe.
Participation des élèves à la reproduction de la synthèse
Définition
- le plan π ainsi identifié à C est appelé plan complexe ou plan Gauss .
- le point P (a, b) qui repère le nombre complexe z=a+bi est l'image de z.
- le nombre complexe z est l'affixe du point P.
- les nombres complexes réels sont repérés par les points de l'axe OX appelé axe réels.
- les nombres imaginaires purs sont repérés par les points de l'axe OY appelé l'axe des imaginaires purs.
REMARQUE
La position de l'image de z est fixée par la longueur du vecteur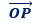 
appelé module de z et par la mesure de l'angle orienté a=
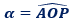appelé argument de z.
L'argument d'un nombre complexe z=a+b est calculé à partir des égalités suivantes:
O est l'argument de z
O est déterminé à un multiple de 2π près.
Forme trigonométrique et exponentielle d'un nombre complexe non nul
soit le nombre complexe z=a+bi.
C'est la forme trigonométrie de z.
En posant 
On obtient:
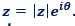C'est la forme exponentielle de z.
Le conjugué de z dans ce cas est:
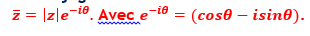
Produit de deux nombres complexe non nul
Soit z1 et z2 deux nombres complexes écrits sous la forme trigonométrique. calculons leur produit:
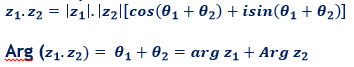
Quotient de deux nombres complexes non nuls
