

Rappel
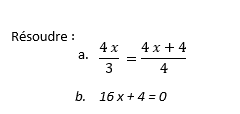
Motivation
Annonce du sujet
Qu'allons-nous étudier aujourd'hui ?
Analyse
Quelle est la forme du système de deux équations à 2 inconnues ?
Citez les méthodes de résolution de ce système.
Comment peut-on procéder à la résolution ?
En quoi consiste la méthode de substitution ?
Comment peut-on effectuer la résolution ?
Qu'est-ce que nous venons de voir ?
Rappel
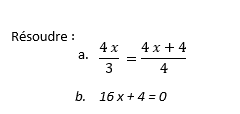

Aujourd'hui, nous allons étudier le système de deux équations à 2 inconnues.
Un système de deux équations à deux inconnues est de la forme : a x + by = c
a ᶦ x + b ᶦ y = c ᶦ
Pour résoudre un système de deux équations à deux inconnues, on doit passer par 4 méthodes qui sont :
Méthode de comparaison
Elle consiste à expliciter chacune de deux équations par rapport à une même inconnue et à comparer (égaler) les deux valeurs trouvées. On obtient une équation à une inconnue. La solution de cette équation, portée dans l'une des équations du système, permet de déterminer la valeur de l'autre inconnue.

Méthode de substitution
Elle consiste à tirer la valeur de l'une des inconnues (y par exemple) de l'une des équations (la première par exemple) et de la porter dans l'autre équation. On obtient une équation à une inconnue. La solution de cette dernière équation sera portée dans l'expression de y pour la déterminer.

Nous venons de voir le système de deux équations à 2 inconnues.